Geometría simpléctica: de los movimientos planetarios a las misiones espaciales

El título de este artículo ya chocará a la mayoría de lectores. Quizá sea especialmente sorprendente la palabra “simpléctica”, que no es de uso común en español y de momento no aparece en el diccionario de la Real Academia Española.  Esta curiosa palabra tiene cada vez mayor arraigo en la investigación matemática española e internacional, y se puede escuchar mencionada en conexión con importantes aplicaciones al mundo real, como es el diseño de misiones espaciales.

El término “simpléctica” fue acuñado en 1939 por Hermann Weyl (1885-1955), eminente matemático alemán y catedrático del Instituto de Estudios Avanzados de Princeton (Estados Unidos). Es una palabra que significa “compleja”, y tiene origen griego. Como la palabra “compleja” ya se usaba ampliamente en matemáticas en relación con los números complejos, para evitar confusión, Weyl propuso el nuevo nombre.

Álvaro Pelayo

Muchos lectores habrán escuchado la palabra “simpléctica” por primera vez en los artículos que han aparecido en los últimos días en la prensa, destacando las contribuciones de Yakov Eliashberg a la geometría simpléctica y Claire Voisin a la geometría algebraica, por las cuales han compartido el Premio Fundación BBVA Fronteras del Conocimiento en su XVI edición. Es de destacar no sólo la importancia de la geometría simpléctica y la geometría algebraica por separado, sino también los puentes que existen entre ambas y sus relaciones con la física teórica y teorías de gran actualidad como la simetría de espejo. Además, como comentaré unas líneas más abajo, la geometría simpléctica tiene notables aplicaciones a los sistemas dinámicos, que estudian la evolución de objetos o variables físicas, económicas, o puramente matemáticas a lo largo del tiempo. Por ejemplo, el movimiento de una hoja desplazada por el viento nos describe un sistema dinámico.

Cuatro grandes áreas de las matemáticas, con profundas interacciones entre ellas

Una rama de las matemáticas con raíces milenarias

Los geómetras en general podemos estar contentos de que el premio reconoce la importancia actual de la geometría. El origen de la geometría está en Euclides y su escuela de la antigua Grecia, alrededor del año 300 a. C. Desde entonces la geometría y sus aplicaciones han evolucionado de modo espectacular. A día de hoy la geometría es una de las grandes áreas de las matemáticas, y tiene una considerable presencia en las grandes escuelas matemáticas del mundo, como pueden ser el Instituto de Estudios Avanzados de Princeton o las Universidades de Stanford, Harvard, California Berkeley, París u Oxford. En Stanford imparte clases Yakov Eliashberg, que es una de las figuras más distinguidas de la geometría simpléctica. En mi caso, conocí al profesor Eliashberg hace unos quince años, cuando coincidíamos regularmente en el seminario de geometría simpléctica del norte de California. Además, juntos organizamos un congreso en honor de otro geómetra, Alan Weinstein, de la Universidad de California Berkeley, institución en la que yo era entonces profesor.

Pero, ¿de qué trata esta geometría con un nombre tan peculiar? Los lectores recordarán que el gran científico y Premio Nobel español Santiago Ramón y Cajal (1852-1934) ya nos deleitaba con sus diagramas y dibujos planos que ilustraban de modo esquemático fenómenos de tres dimensiones sobre el cerebro humano. Grosso modo, mientras que para un científico del cerebro puede resultar útil esquematizar y dibujar secciones planas (es decir, bidimensionales) del cerebro (que es tridimensional), un geómetra simpléctico hace lo análogo con objetos multidimensionales de cualquier dimensión par. Esta esquematización corresponde a hacer mediciones de áreas de secciones bidimensionales de dichos objetos, como si cortáramos una naranja y nos fijáramos en la sección abierta que resulta.

Secciones bidimensionales de un objeto tridimensional, en analogía con las mediciones de área de secciones
bidimensionales de objetos multidimensionales que hace la geometría simpléctica.

Por tanto, podemos decir que la geometría simpléctica se basa en un uso sofisticado del concepto de área, lo que contrasta con la geometría euclidiana y casi todos los tipos de geometría, que están más basados en los conceptos de longitud/distancia o volumen. Como materia, la geometría simpléctica está bajo el paraguas de la geometría diferencial. Es decir, resuelve problemas utilizando principalmente métodos del cálculo diferencial de Newton y Leibniz como las famosas derivadas e integrales estudiadas en bachillerato (aunque es cierto que cada vez incorpora más herramientas de álgebra, topología, análisis matemático y otras disciplinas).

La geometría simpléctica es una geometría muy especial en tanto que comparte facetas de rigidez, que por ejemplo exhibe la geometría euclidiana, con facetas de flexibilidad. En este sentido involucra una combinación de fenómenos de naturaleza cualitativa con otros de naturaleza cuantitativa. Por ejemplo, podemos decir que un círculo y el mismo círculo deformado son similares cualitativamente. Sin embargo, las distancias entre los puntos que forman el círculo pueden haber cambiado con la deformación, y por tanto la situación ha cambiado cuantitativamente. La geometría, en general, tiene una ventaja sobre otras partes de las matemáticas, y es que se ve: se puede dibujar, se puede ilustrar. En este sentido, muchos aspectos de la geometría son intuitivos. Sin embargo, al estar enfocada en objetos multidimensionales, principalmente de dimensión cuatro o mayor, la geometría simpléctica es menos intuitiva.

Puede resultar chocante, quizás incluso extraño, que, siendo menos intuitiva, la geometría simpléctica esté conectada con el mundo físico. De hecho, se origina en los estudios de los movimientos planetarios llevados a cabo por los grandes científicos Leonhard Euler (1707–1883), Galileo Galilei (1564-1642), Christiaan Huygens (1629–1695), Joseph-Louis Lagrange (1736-1813) e Isaac Newton (1643-1727) hace más de trescientos años. Por ello, no es una mera invención matemática, sino más bien todo lo contrario.

El Teorema de Poincaré-Birkhoff, la base de la geometría simpléctica

El punto de vista moderno en geometría simpléctica se remonta al sabio francés Henri Poincaré (1854-1912), en sus estudios de mecánica celeste, y más en concreto al famoso teorema conocido como el Teorema de Poincaré-Birkhoff. Este gran teorema fue enunciado y probado en algunos casos por Poincaré en 1912 y demostrado con completa generalidad por Birkhoff en 1913. El resultado parte de una anilla elástica, hecha por ejemplo de goma o de un material deformable. Imaginemos que, con una mano, giramos el círculo interno en una dirección, y con la otra mano giramos el externo en la dirección opuesta. Pues bien, el Teorema garantiza que siempre hay al menos dos puntos que no se mueven de su posición inicial, por muy complicada que sea la deformación que hacemos, como en la figura:

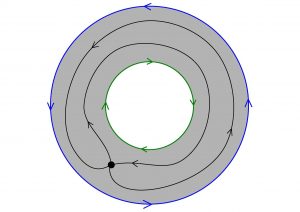
Ilustración geométrica del Teorema de Poincaré-Birkhoff (1913), origen de la geometría simpléctica moderna

Es importante observar varias cosas sobre este resultado. Primero, el que la deformación preserve área quiere decir que si hay, por ejemplo, una nube pintada en la anilla, después de la deformación, la nube deformada tiene la misma área que la original. Segundo, la forma global de la anilla tiene que permanecer la misma durante la deformación. Los que pueden cambiar de lugar, y de hecho lo harán en casi cualquier deformación, son los puntos de la anilla. La maravilla del teorema es que nos garantiza que hay al menos dos puntos que no cambian de posición.

El Teorema de Poincaré-Birkhoff, que es de dos dimensiones, se generaliza a cualquier dimensión par, y en ese caso, se conoce como la Conjetura de Arnold, que es de los años 1960 y que fue formulada por el matemático ruso Vladimir Arnold (1937-2010). La conjetura, que es una de las fuerzas precursoras de la geometría simpléctica moderna, nos garantiza un cierto número mínimo de puntos fijos para las deformaciones en dimensiones superiores.

A partir de la Conjectura de Arnold, y otros descubrimientos que tuvieron lugar en las décadas de los años 1970, 1980 y 1990, con trabajos de muchos matemáticos eminentes como Charles Conley, Hans Duistermaat, Yakov Eliashberg, Andreas Floer, Alexander Givental, Victor Guillemin, Mikhael Gromov, Helmut Hofer, Bertram Kostant, Paulette Libermann, Dusa McDuff, Jean-Marie Souriau, Shlomo Sternberg, Alan Weinstein y Eduard Zehnder, la geometría simpléctica se consolidó como una de las grandes áreas de las matemáticas modernas. En España, uno de los primeros expertos (en concreto en la conexión con la física) fue Pedro Luis García Pérez, de la Universidad de Salamanca. Ha habido tantos desarrollos en las últimas décadas, que mencionarlos incluso superficialmente está fuera de los objetivos de nuestro breve artículo divulgativo.

Sin embargo, a modo representativo es imposible no citar que el premiado por la Fundación BBVA, Yakov Eliashberg, lleva décadas haciendo contribuciones importantes a la geometría simpléctica, así como a áreas cercanas como la geometría de contacto y la topología. Por ejemplo, su trabajo sobre el fenómeno de rigidez simpléctica al principio de los años 1980 es un hito fundamental. De hecho, los principios de los años 1980 fueron una época extraordinaria, con la demostración de Conley y Zehnder de la Conjetura de Arnold para el toro (un objeto geométrico en forma de rosquilla), y la demostración del teorema de no-estrujamiento por Gromov.

Para dar una idea de este último resultado, imaginemos que queremos meter una pelota sólida dentro de un cilindro infinitamente largo, pero de diámetro menor que el de la pelota. Supongamos también que la pelota es de gomaespuma, así que podemos estrujarla para que, aunque ocupe siempre el mismo volumen, esté alargada de forma que quepa dentro del cilindro. Pues bien, el Teorema de Gromov nos dice que, aunque tengamos éxito metiendo la bola dentro del cilindro manteniendo su volumen inicial, al estrujarla hemos cambiado necesariamente las áreas de las secciones bidimensionales (recordemos: aquellas que resultan de cortar la pelota en rodajas). Por tanto, desde el punto de vista de la geometría simpléctica, la pelota no se puede estrujar en un cilindro con menor radio (de ahí que este resultado se conozca como teorema de no-estrujamiento). En realidad, el teorema se refiere a pelotas y cilindros de dimensión 4 o mayor, pero sirva esta analogía más visual para captar la esencia del resultado.

Ha habido muchos otros resultados importantes en geometría simpléctica en las últimas décadas, algunos son fascinantes en cuanto que establecen puentes entre ella y otros mundos de las matemáticas, como el mundo de los polígonos y sus generalizaciones a dimensiones mayores, los politopos. En la conferencia que impartí en la Real Academia de Ciencias Exactas, Físicas y Naturales comento algunos de estos trabajos, realizados por Michael Atiyah y los ya mencionados Guillemin y Sternberg en los años 1980.

Las matemáticas que salvaron una misión espacial

Aunque todos estos resultados nos parezcan muy interesantes, es natural preguntarse si la geometría simpléctica tiene aplicaciones al mundo real. La respuesta es afirmativa de modo rotundo: se aplica a la física del plasma, la teoría de la elasticidad, la robótica, la mecánica de fluidos y al diseño de misiones espaciales, entre otras muchas materias.

De hecho, la geometría simpléctica fue esencial para salvar una misión espacial que se daba por perdida. En 1990, la Agencia Espacial Japonesa lanzó una gran astronave al espacio, que se separó en dos. Su objetivo era poner una de ellas en órbita alrededor de la Luna. Pero, debido a una avería, la perdieron. Su única esperanza para salvar la misión era poner la otra en órbita alrededor de la Luna, pero no había suficiente combustible para ello. El matemático Edward Belbruno se enteró del problema y aportó una ingeniosa solución, basada en principios básicos de geometría simpléctica y sistemas dinámicos, para conseguir que la nave entrase (aprovechando, entre otras cosas, las fuerzas gravitatorias del Sol y de la Tierra) en la órbita lunar que se buscaba con el poco combustible que quedaba, salvando así la misión.

A día de hoy, los métodos avanzados de geometría simpléctica que han desarrollado Yakov Eliashberg, Helmut Hofer y sus colaboradores y escuelas se están tratando de aplicar, en colaboración con importantes agencias espaciales, para la optimización de las trayectorias a seguir por las naves espaciales, de tal modo que se use el mínimo combustible posible.